Find all the angles of an equilateral triangle.

Solution:

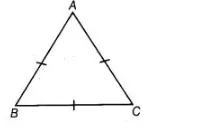
Let $A B C$ be an equilateral triangle such that $A B=B C=C A$

We have, $\quad A B=A C \Rightarrow \angle C=\angle B$

[angles opposite to equal sides are equal]

Let $\angle C=\angle B=x^{\circ}$ $\ldots(i)$

Now, $B C=B A$

$\Rightarrow$ $\angle A=\angle C$ ... (ii)

[angles opposite to equal sides are equal]

From Eqs. (i) and (ii),

$\angle A=\angle B=\angle C=x$

Now, in $\triangle A B C$, $\angle A+\angle B+\angle C=180^{\circ}$ [by angle sum property of a triangle]

$\Rightarrow \quad x+x+x=180^{\circ}$

$\Rightarrow \quad 3 x=180^{\circ}$

$\therefore \quad x=60^{\circ}$ 

Hence, $\angle A=\angle B=\angle C=60^{\circ}$