Question:
Find the area bounded by the curve $y=\sin x$ between $x=0$ and $x=2 \pi$
Solution:
The graph of y = sin x can be drawn as
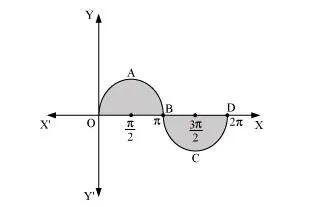
$\therefore$ Required area = Area OABO + Area BCDB
$=\int_{0}^{\pi} \sin x d x+\left|\int_{\pi}^{2 \pi} \sin x d x\right|$
$=[-\cos x]_{0}^{\pi}+\left|[-\cos x]_{\pi}^{2 \pi}\right|$
$=[-\cos \pi+\cos 0]+|-\cos 2 \pi+\cos \pi|$
$=1+1+|(-1-1)|$
$=2+|-2|$
$=2+2=4$ units
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.