Find the area of quad. ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diag.

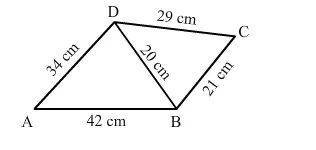
Quadrilateral $A B C D$ is divided into triangles $\triangle A B D$ and $\triangle B C D$.

We will now use Hero's formula.

For $\triangle A B D$ :

Semiperimeter, $s=\frac{1}{2}(42+20+34)=\frac{96}{2}=48 \mathrm{~cm}$

Area of $\Delta \mathrm{ABD}=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{48(48-42)(48-34)(48-20)}$

$=\sqrt{48 \times 6 \times 14 \times 28}$

$=\sqrt{112896}$

$=336 \mathrm{~cm}^{2}$

For $\triangle B C D$ :

$s=\frac{1}{2}(20+21+29)=\frac{70}{2}=35 \mathrm{~cm}$

Area of $\Delta \mathrm{BCD}=\sqrt{s(s-a)(s-b)(s-c)}$

$=\sqrt{35(35-20)(35-21)(35-29)}$

$=\sqrt{35 \times 15 \times 14 \times 6}$

$=\sqrt{44100}$

$=210 \mathrm{~cm}^{2}$

Thus, we have:

Area of quadrilateral $A B C D=\operatorname{Ar}(\Delta A B D)+\operatorname{Ar}(B D C)=336+210=546 \mathrm{~cm}^{2}$