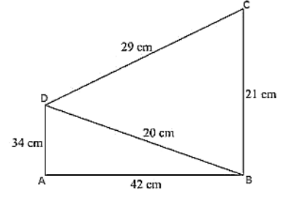
Find the area of quadrilateral ABCD in which AB = 42 cm, BC = 21 cm, CD = 29 cm,

Given

AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm, and the diagonal

BD = 20 cm.

Now, for the area of triangle ABD

Perimeter of triangle ABD 2s = AB + BD + DA

2s = 34 cm + 42 cm + 20 cm

s = 48 cm

By using Heron’s Formula,

Area of the triangle $\mathrm{ABD}=\sqrt{\mathrm{s} \times(\mathrm{s}-\mathrm{a}) \times(\mathrm{s}-\mathrm{b}) \times(\mathrm{s}-\mathrm{c})}$

$=\sqrt{48 \times(48-42) \times(48-20) \times(48-34)}$

$=336 \mathrm{~cm}^{2}$

Now, for the area of triangle BCD

Perimeter of triangle BCD 2s = BC + CD + BD

2s = 29cm + 21cm + 20cm

s = 35 cm

By using Heron's Formula,

Area of the triangle $\mathrm{BCD}=\sqrt{\mathrm{s} \times(\mathrm{s}-\mathrm{a}) \times(\mathrm{s}-\mathrm{b}) \times(\mathrm{s}-\mathrm{c})}$

$=\sqrt{35 \times(14) \times(6) \times(15)}$

$=210 \mathrm{~cm}^{2}$

Therefore, Area of quadrilateral ABCD = Area of triangle ABD + Area of triangle BCD

Area of quadrilateral ABCD = 336 + 210

Area of quadrilateral $\mathrm{ABCD}=546 \mathrm{~cm}^{2}$