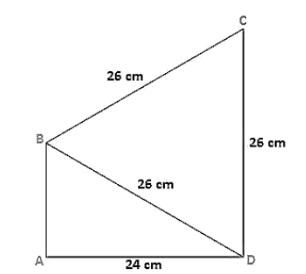
Find the area of the quadrilateral $\mathrm{ABCD}$ in which $\mathrm{AD}=24 \mathrm{~cm}$, angle $\mathrm{BAD}=90^{\circ}$ and $\mathrm{BCD}$ forms an equilateral triangle whose each side is equal to $26 \mathrm{~cm}$. [Take $\sqrt{3}=1.73$ ]
Given that, in a quadrilateral ABCD in which AD = 24 cm,
Angle BAD = 90°
BCD is an equilateral triangle and the sides BC = CD = BD = 26 cm
In triangle BAD, by applying Pythagoras theorem,
$B A^{2}=B D^{2}-A D^{2}$
$B A^{2}=26^{2}+242$
$B A=\sqrt{100}$
$B A=10 \mathrm{~cm}$
Area of the triangle BAD = 1/2 × BA × AD
Area of the triangle BAD = 1/2 × 10 × 24
Area of the triangle BAD $=120 \mathrm{~cm}^{2}$
Area of the equilateral triangle $=\sqrt{3} / 4 \times$ side
Area of the equilateral triangle $\mathrm{QRS}=\sqrt{3 / 4} \times 26$
Area of the equilateral triangle $B C D=292.37 \mathrm{~cm}^{2}$
Therefore, the area of quadrilateral $A B C D=$ Area of triangle $B A D+$ Area of the triangle BCD
The area of quadrilateral $A B C D=120+292.37$
$=412.37 \mathrm{~cm}^{2}$