Question.
Find the area of the quadrilateral whose vertices taken in order are (–4, –2), (–3, –5), (3, –2) and (2, 3).
Find the area of the quadrilateral whose vertices taken in order are (–4, –2), (–3, –5), (3, –2) and (2, 3).
Solution:
Join A and C. The given points are
$\mathrm{A}(-4,-2), \mathrm{B}(-3,-5), \mathrm{C}(3,-2)$ and $\mathrm{D}(2,3)$
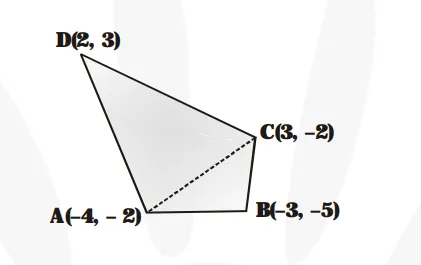
Area of $\triangle \mathrm{ABC}$
$=\frac{\mathbf{1}}{\mathbf{2}}[(-4)(-5+2)-3(-2+2)+3(-2+5)]$
$=\frac{\mathbf{1}}{\mathbf{2}}[12+0+9]=\frac{\mathbf{2 1}}{\mathbf{2}}=10.5$ sq. units
Area of $\Delta \mathrm{ACD}$
$=\frac{1}{2}[(-4)(-2-3)+3(3+2)+2(-2+2)]$
$=\frac{\mathbf{1}}{\mathbf{2}}\left[20+15 \mid=\frac{\mathbf{3 5}}{\mathbf{2}}=17.5\right.$ sq. units.
Area of quadrilateral ABCD
$=\operatorname{ar}(\Delta \mathrm{ABC})+\operatorname{ar}(\Delta \mathrm{ACD})$
$=(10.5+17.5) \mathrm{sq} .$ units $=28 \mathrm{sq} .$ units
Join A and C. The given points are
$\mathrm{A}(-4,-2), \mathrm{B}(-3,-5), \mathrm{C}(3,-2)$ and $\mathrm{D}(2,3)$

Area of $\triangle \mathrm{ABC}$
$=\frac{\mathbf{1}}{\mathbf{2}}[(-4)(-5+2)-3(-2+2)+3(-2+5)]$
$=\frac{\mathbf{1}}{\mathbf{2}}[12+0+9]=\frac{\mathbf{2 1}}{\mathbf{2}}=10.5$ sq. units
Area of $\Delta \mathrm{ACD}$
$=\frac{1}{2}[(-4)(-2-3)+3(3+2)+2(-2+2)]$
$=\frac{\mathbf{1}}{\mathbf{2}}\left[20+15 \mid=\frac{\mathbf{3 5}}{\mathbf{2}}=17.5\right.$ sq. units.
Area of quadrilateral ABCD
$=\operatorname{ar}(\Delta \mathrm{ABC})+\operatorname{ar}(\Delta \mathrm{ACD})$
$=(10.5+17.5) \mathrm{sq} .$ units $=28 \mathrm{sq} .$ units
