Find the area of the shaded region in fig.,

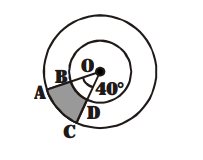
Radius of the outer circle $=14 \mathrm{~cm}$ and $\theta=40^{\circ}$

$\therefore \quad$ Area of the sector $\mathrm{AOC}$

$=\frac{40^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 14 \times 14 \mathrm{~cm}^{2}$

$=\frac{1}{9} \times 22 \times 2 \times 14 \mathrm{~cm}^{2}=\frac{616}{9} \mathrm{~cm}^{2}$

Radius of the inner circle $=7 \mathrm{~cm}$ and $\theta=40^{\circ}$

$\therefore$ Area of the sector BOD

$=\frac{40^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 7 \times 7 \mathrm{~cm}^{2}$

$=\frac{1}{9} \times 22 \times 7 \mathrm{~cm}^{2}=\frac{154}{9} \mathrm{~cm}^{2}$

Now, area of the shaded region

= Area of sector AOC – Area of sector BOD 

$=\frac{\mathbf{6 1 6}}{\mathbf{9}}-\frac{\mathbf{1 5 4}}{\mathbf{9}} \mathrm{cm}^{2}=\frac{\mathbf{1}}{\mathbf{9}}(616-154) \mathrm{cm}^{2}$

$=\frac{1}{9} \times 462 \mathrm{~cm}^{2}=\frac{154}{3} \mathrm{~cm}^{2}$