Find the area of the shaded region in fig, if

Solution:

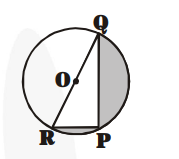
In the figure, $\angle \mathrm{RPQ}=90^{\circ}$

(Angle subtended by a diameter on the circumference)

Therefore, $\triangle R P Q$ is right angled at $P$,

RP = 7 cm and PQ = 24 cm

Then by Pythagoras Theorem, we have 

$\mathrm{QR}^{2}=\mathrm{RP}^{2}+\mathrm{PQ}^{2}$

$\mathrm{QR}^{2}=\mathrm{RP}^{2}+\mathrm{PQ}^{2}$

$=(7)^{2}+(24)^{2}=625$

$\Rightarrow \mathrm{QR}=25 \mathrm{~cm}$

$\therefore$ The radius of the circle

$=\frac{25}{2} \mathrm{~cm}$

Now, the area of the shaded region (see figure)

$=\frac{1}{2} \pi r^{2}-\frac{1}{2} \times R P \times P Q$

$=\left\{\frac{1}{2} \times \frac{22}{7} \times\left(\frac{25}{2}\right)^{2}-\frac{1}{2} \times 7 \times 24\right\} \mathrm{cm}^{2}$

$=\left\{\frac{6875}{28}-84\right\} c m^{2}=\frac{4523}{28} \mathrm{~cm}^{2}$