Find the area of the shaded region in figure,

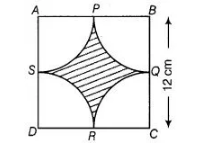
Given, side of a square BC = 12 cm

Since, Q is a mid-point of BC

$\therefore$ Radius $=B Q=\frac{12}{2}=6 \mathrm{~cm}$

Now, $\quad$ area of quadrant $B P Q=\frac{\pi r^{2}}{4}=\frac{3.14 \times(6)^{2}}{4}=\frac{113.04}{4} \mathrm{~cm}^{2}$

Area of four quadrants $=\frac{4 \times 113.04}{4}=1123.04 \mathrm{~cm}^{2}$

Now, $\quad$ area of square $A B C D=(12)^{2}=144 \mathrm{~cm}^{2}$

$\therefore$ Area of the shaded region $=$ Area of square $-$ Area of four quadrants

$=144-113.04=30.96 \mathrm{~cm}^{2}$