Find the area of the triangle formed by the lines

The given equations are

$x=0 \ldots(\mathrm{i})$

$y=1 \ldots(\mathrm{ii})$

and $2 x+y=2 \ldots$ (iii)

Let eq. (i), (ii) and (iii) represents the sides AB, BC and AC respectively of ΔABC

From eq. (i) and (ii), we get $x=0$ and $y=1$

Thus, $A B$ and $B C$ intersect at $(0,1)$

Solving eq. (ii) and (iii), we get

$y=1 \ldots$ (ii)

and $2 x+y=2 \ldots$ (iii)

Putting the value of y = 1 in eq. (iii), we get

$2 x+1=2$

$\Rightarrow 2 x=1$

$\Rightarrow x=\frac{1}{2}$

Thus, $\mathrm{BC}$ and $\mathrm{AC}$ intersect at $\left(\frac{1}{2}, 1\right)$

Now, Solving eq. (iii) and (i), we get

$2 x+y=2 \ldots$ (iii)

and $x=0 \ldots$ (i)

Putting the value of x = 0 in eq. (iii), we get

y = 2

Thus, AC and AB intersect at (0, 2)

So, vertices of triangle $\mathrm{ABC}$ are : $(0,1),\left(\frac{1}{2}, 1\right)$ and $(0,2)$

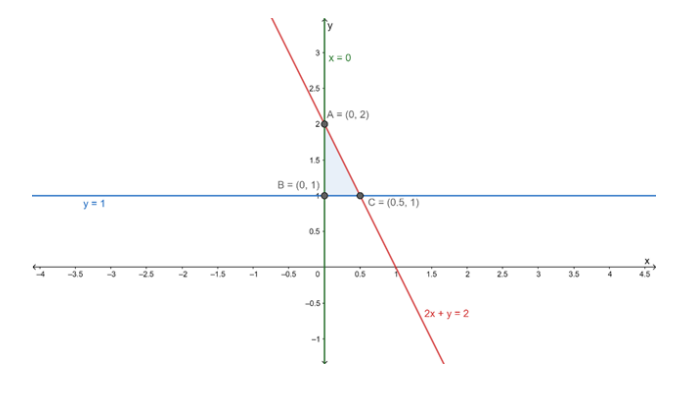
$\therefore$ Area of $\triangle \mathrm{ABC}=\frac{1}{2} \times$ base $\times$ height

$=\frac{1}{2} \times \frac{1}{2} \times 1$

$=\frac{1}{4} \mathrm{sq} .$ units