Find the area of the triangle formed by the lines joining the vertex of the parabola

The given parabola is $x^{2}=12 y$.

On comparing this equation with $x^{2}=4 a y$, we obtain $4 a=12 \Rightarrow a=3$

$\therefore$ The coordinates of foci are $S(0, a)=S(0,3)$

Let AB be the latus rectum of the given parabola.

The given parabola can be roughly drawn as

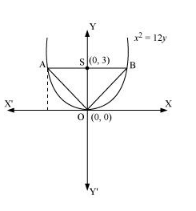
At $y=3, x^{2}=12(3) \Rightarrow x^{2}=36 \Rightarrow x=\pm 6$

$\therefore$ The coordinates of $A$ are $(-6,3)$, while the coordinates of $B$ are $(6,3)$.

Therefore, the vertices of $\triangle O A B$ are $O(0,0), A(-6,3)$, and $B(6,3)$.

Area of $\triangle \mathrm{OAB}=\frac{1}{2}|0(3-3)+(-6)(3-0)+6(0-3)|$ unit $^{2}$

$=\frac{1}{2}|(-6)(3)+6(-3)|$ unit $^{2}$

$=\frac{1}{2}|-18-18|$ unit $^{2}$

$=\frac{1}{2}|-36|$ unit $^{2}$

$=\frac{1}{2} \times 36$ unit $^{2}$

$=18$ unit $^{2}$

Thus, the required area of the triangle is 18 unit $^{2}$.