Find the area of the triangle, the equations

The given equations are

$y=x \ldots$ (i)

$y=2 x \ldots$ (ii)

and $y-3 x=4 \ldots$ (iii)

Let eq. (i), (ii) and (iii) represents the sides $A B, B C$ and $A C$ respectively of $\triangle A B C$

From eq. (i) and (ii), we get $x=0$ and $y=0$

Thus, $A B$ and $B C$ intersect at $(0,0)$

Solving eq. (ii) and (iii), we get

$\mathrm{y}=2 \mathrm{x} \ldots$ (ii)

and $y-3 x=4 \ldots$ (iii)

Putting the value of y = 2x in eq. (iii), we get

$2 x-3 x=4$

$\Rightarrow-x=4$

$\Rightarrow x=-4$

Putting the value of x = -4 in eq. (ii), we get

$y=2(-4)$

$\Rightarrow y=-8$

Thus, $B C$ and $A C$ intersect at $(-4,-8)$

Now, Solving eq. (iii) and (i), we get

$y-3 x=4 \ldots$ (iii)

and $y=x \ldots$ (i)

Putting the value of y = x in eq. (iii), we get

$x-3 x=4$

$\Rightarrow-2 x=4$

$\Rightarrow x=-2$

Putting the value of x = -2 in eq. (i), we get

$y=-2$

Thus, $A C$ and $A B$ intersect at $(-2,-2)$

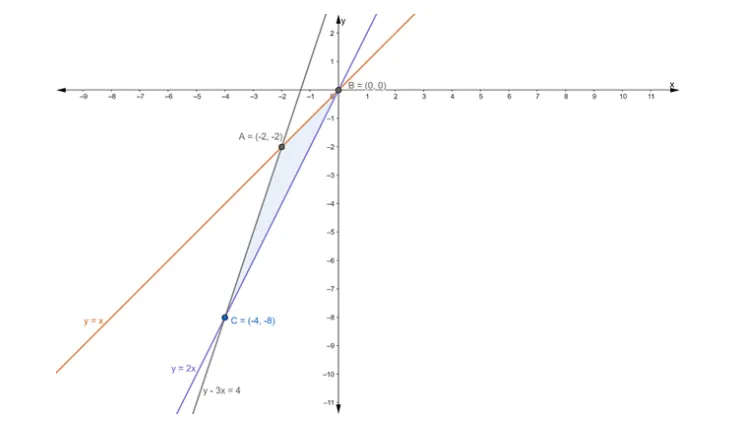
So, vertices of triangle $\mathrm{ABC}$ are: $(0,0),(-4,-8)$ and $(-2,-2)$

$\therefore$ Area of $\Delta \mathrm{ABC}=\frac{1}{2}\left|\begin{array}{ccc}0 & 0 & 1 \\ -2 & -2 & 1 \\ -4 & -8 & 1\end{array}\right|$

$=\frac{1}{2}[0-0+1\{(-2)(-8)-(-2)(-4)\}]$

$=\frac{1}{2}[1\{16-8\}]$

$=\frac{1}{2}[8]$

$=4 \mathrm{sq} .$ units