Find the condition for the following set of curves to interest orthogonally.

Given:

Curves $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ ..(1)

$\& \frac{x^{2}}{A^{2}}-\frac{y^{2}}{B^{2}}=1$     ....(2)

First curve is $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$

Differentiating above w.r.t $x$,

$\Rightarrow \frac{2 x}{a^{2}}-\frac{2 y}{b^{2}} \cdot \frac{d y}{d x}=0$

$\Rightarrow \frac{y}{b^{2}} \cdot \frac{d y}{d x}=\frac{x}{a^{2}}$

$\Rightarrow \frac{d y}{d x}=\frac{\frac{x}{a^{2}}}{\frac{y^{2}}{b^{2}}}$

$\Rightarrow \frac{d y}{d x}=\frac{b^{2} x}{a^{2} y}$

$\Rightarrow m_{1}=\frac{b^{2} x}{a^{2} y} \ldots(3)$

Second curve is $\frac{x^{2}}{A^{2}}-\frac{y^{2}}{B^{2}}=1$

Differentiating above w.r.t $x$,

$\Rightarrow \frac{2 x}{A^{2}}-\frac{2 y}{B^{2}} \cdot \frac{d y}{d x}=0$

$\Rightarrow \frac{y}{B^{2}} \cdot \frac{d y}{d x}=\frac{x}{A}$

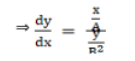
$\Rightarrow \frac{d y}{d x}=\frac{B^{2} x}{A^{2} y}$

$\Rightarrow m_{1}=\frac{B^{2} x}{A^{2} y} \ldots(4)$

When $m_{1}=\frac{b^{2} x}{a^{2} y} \& m_{2}=\frac{B^{2} x}{A^{2} y}$

Since, two curves intersect orthogonally,

$\Rightarrow \frac{\mathrm{b}^{2} \mathrm{x}}{\mathrm{a}^{2} \mathrm{y}} \times \frac{\mathrm{B}^{2} \mathrm{x}}{\mathrm{A}^{2} \mathrm{y}}=-1$

$\Rightarrow \frac{\mathrm{b}^{2} \mathrm{~B}^{2}}{\mathrm{a}^{2} \mathrm{~A}^{2}} \times \frac{\mathrm{x}^{2}}{\mathrm{y}^{2}}=-1$

$\Rightarrow \frac{\mathrm{x}^{2}}{\mathrm{y}^{2}}=\frac{-\mathrm{a}^{2} \mathrm{~A}^{2}}{\mathrm{~b}^{2} \mathrm{~B}^{2}} \ldots(5)$

Now equation (1) - (2) gives

$\Rightarrow\left(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\right)-\left(\frac{x^{2}}{A^{2}}-\frac{y^{2}}{B^{2}}=1\right)$

$\Rightarrow x^{2}\left(\frac{1}{a^{2}}-\frac{1}{A^{2}}\right)-y^{2}\left(\frac{1}{b^{2}}-\frac{1}{B^{2}}\right)=0$

$\Rightarrow x^{2}\left(\frac{1}{a^{2}}-\frac{1}{A^{2}}\right)=y^{2}\left(\frac{1}{b^{2}}-\frac{1}{B^{2}}\right)$

$\Rightarrow \frac{x^{2}}{y^{2}}=\frac{\left(\frac{1}{b^{2}}-\frac{1}{B^{2}}\right)}{\left(\frac{1}{a^{2}}-\frac{1}{A^{2}}\right)}$

$\Rightarrow \frac{x^{2}}{y^{2}}=\frac{\left(\frac{B^{2}-b^{2}}{b^{2} B^{2}}\right)}{\left(\frac{A^{2}-a^{2}}{A^{2} a^{2}}\right)}$

$\Rightarrow \frac{x^{2}}{y^{2}}=\frac{\left(B^{2}-b^{2}\right)\left(A^{2} a^{2}\right)}{\left(A^{2}-a^{2}\right)\left(b^{2} B^{2}\right)}$

Substituting $\frac{x^{2}}{y^{2}}$ from equation $(5)$, we get

$\Rightarrow \frac{-a^{2} A^{2}}{b^{2} B^{2}}=\frac{\left(B^{2}-b^{2}\right)\left(A^{2} a^{2}\right)}{\left(A^{2}-a^{2}\right)\left(b^{2} B^{2}\right)}$

$\Rightarrow-1=\frac{\left(\mathrm{B}^{2}-\mathrm{b}^{2}\right)}{\left(\mathrm{A}^{2}-\mathrm{a}^{2}\right)}$

$\Rightarrow(-1)\left(A^{2}-a^{2}\right)=\left(B^{2}-b^{2}\right)$

$\Rightarrow a^{2}-A^{2}=B^{2}-b^{2}$

$\Rightarrow a^{2}+b^{2}=B^{2}+A^{2}$