Question:
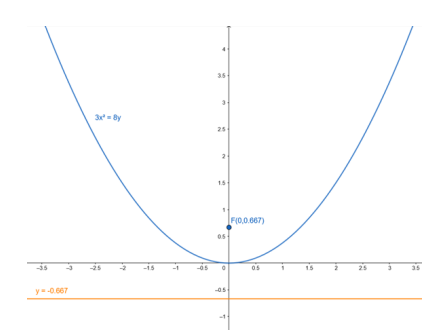
Find the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola :
$3 x^{2}=8 y$
Solution:
Given equation :
$3 x^{2}=8 y$
$x^{2}=\frac{8}{3} y$
Comparing the given equation with parabola having an equation,
$x^{2}=4 a y$
$\cdot 4 a=\frac{8}{3}$
- $a=\frac{2}{3}$
Focus: $F(0, a)=F\left(0, \frac{2}{3}\right)$
Vertex : $A(0,0)=A(0,0)$
Equation of the directrix: $y+a=0$
$y+\frac{2}{3}=0$
$y=-\frac{2}{3}$
Lenth of latusrectum :
$4 a=\frac{8}{3}$