Question:
Find the coordinates of the focus and the vertex, the equations of the directrix and the axis, and length of the latus rectum of the parabola :
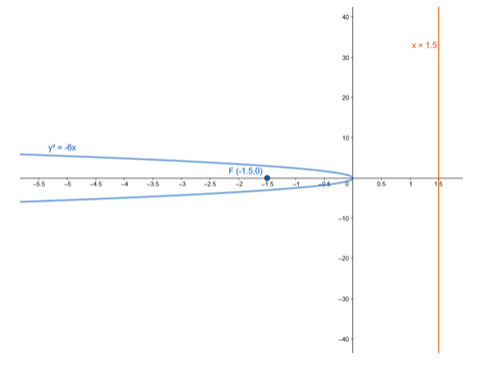
$y^{2}=-6 x$
Solution:
Given equation :
$y^{2}=-6 x$
Comparing given equation with parabola having equation,
$y^{2}=-4 a x$
$4 a=6$
$\cdot a=\frac{3}{2}$
Focus: $F(-a, 0)=F\left(-\frac{3}{2}, 0\right)$
Vertex: $A(0,0)=A(0,0)$
Equation of the directrix : $x-a=0$
$x-\frac{3}{2}=0$
$\mathrm{X}=\frac{3}{2}$
Lenth of latusrectum : $4 a=6$
