Find the difference of the areas of a sector

Given that, radius of the circle (r) = 21 cm and central angle of the sector AOBA (θ) = 120°

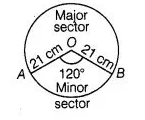
So, area of the circle $=\pi r^{2}=\frac{22}{7} \times(21)^{2}=\frac{22}{7} \times 21 \times 21$

$=22 \times 3 \times 21=1386 \mathrm{~cm}^{2}$

Now, area of the minor sector $A O B A$ with central angle $120^{\circ}$

$=\frac{\pi r^{2}}{360^{\circ}} \times \theta=\frac{22}{7} \times \frac{21 \times 21}{360^{\circ}} \times 120$

$=\frac{22 \times 3 \times 21}{3}=22 \times 21=462 \mathrm{~cm}^{2}$

$\therefore$ Area of the major sector $A B O A$

$=$ Area of the circle $-$ Area of the sector $A O B A$

$=1386-462=924 \mathrm{~cm}^{2}$

$\therefore$ Difference of the areas of a sector $A O B A$ and its corresponding major sector $A B O A$

$=\mid$ Area of major sector $A B O A-$ Area of minor sector $A O B A \mid$

$=|924-462|=462 \mathrm{~cm}^{2}$

Hence, the required difference of two sectors is 462 cm²