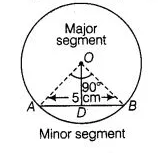
Find the difference of the areas of two segments

Let the radius of the circle be r

$\therefore$ $O A=O B=r \mathrm{~cm}$

Given that, length of chord of a circle, $A B=5 \mathrm{~cm}$ and central angle of the sector $A O B A(\theta)=90^{\circ}$

Now, in $\triangle A O B$ $(A B)^{2}=(O A)^{2}+(O B)^{2}$ [by Pythagoras theorem]

$(5)^{2}=r^{2}+r^{2}$

$\Rightarrow$ $2 r^{2}=25$

$\therefore$ $r=\frac{5}{\sqrt{2}} \mathrm{~cm}$

Now, in $\triangle A O B$ we drawn a perpendicular line $O D$, which meets at $D$ on $A B$ and divides chord $A B$ into two equal parts.

So, $A D=D B=\frac{A B}{2}=\frac{5}{2} \mathrm{~cm}$

[since, the perpendicular drawn from the centre to the chord of a circle divides the chord into two equal parts]

By Pythagoras theorem, in $\triangle A D O$,

$(O A)^{2}=O D^{2}+A D^{2}$

$\Rightarrow \quad O D^{2}=O A^{2}-A D^{2}$

$=\left(\frac{5}{\sqrt{2}}\right)^{2}-\left(\frac{5}{2}\right)^{2}=\frac{25}{2}-\frac{25}{4}$

$=\frac{50-25}{4}=\frac{25}{4}$

$\Rightarrow$ $O D=\frac{5}{2} \mathrm{~cm}$

$\therefore$ Area of an isosceles $\Delta A O B=\frac{1}{2} \times$ Base $(=A B) \times$ Height $(=O D)$

$=\frac{1}{2} \times 5 \times \frac{5}{2}=\frac{25}{4} \mathrm{~cm}^{2}$

Now, area of sector $A O B A=\frac{\pi r^{2}}{360^{\circ}} \times \theta=\frac{\pi \times\left(\frac{5}{\sqrt{2}}\right)^{2}}{360^{\circ}} \times 90^{\circ}$

$=\frac{\pi \times 25}{2 \times 4}=\frac{25 \pi}{8} \mathrm{~cm}^{2}$

$\therefore$ Area of minor segment $=$ Area of sector $A O B A$ - Area of an isosceles $\triangle A O B$

$=\left(\frac{25 \pi}{8}-\frac{25}{4}\right) \mathrm{cm}^{2}$ ...(i)

Now, area of the circle $=\pi r^{2}=\pi\left(\frac{5}{\sqrt{2}}\right)=\frac{25 \pi}{2} \mathrm{~cm}^{2}$

$\therefore$ Area of major segment $=$ Area of circle $-$ Area of minor segment

$=\frac{25 \pi}{2}-\left(\frac{25 \pi}{8}-\frac{25}{4}\right)$

$=\frac{25 \pi}{8}(4-1)+\frac{25}{4}$

$=\left(\frac{75 \pi}{8}+\frac{25}{4}\right) \mathrm{cm}^{2}$$\ldots($ i)

$\therefore$ Difference of the areas of two segments of a circle $=\mid$ Area of major segment - Area of minor segment|

$=\left|\left(\frac{75 \pi}{8}+\frac{25}{4}\right)-\left(\frac{25 \pi}{4}-\frac{25}{4}\right)\right|$

$=\left|\left(\frac{75 \pi}{8}-\frac{25 \pi}{8}\right)-\left(\frac{25 \pi}{8}+\frac{25}{4}\right)\right|$

$=\left|\frac{75 \pi-25 \pi}{8}+\frac{50}{4}\right|=\left|\frac{50 \pi}{8}+\frac{50}{4}\right|$

$=\left(\frac{25 \pi}{4}+\frac{25}{2}\right) \mathrm{cm}^{2}$

Hence, the required difference of the areas of two segments is $\left(\frac{25 \pi}{4}+\frac{25}{2}\right) \mathrm{cm}^{2}$