Find the direction cosines of the sides of the triangle whose vertices are (3, 5, − 4), (− 1, 1, 2) and (− 5, − 5, − 2)

The vertices of ΔABC are A (3, 5, −4), B (−1, 1, 2), and C (−5, −5, −2).

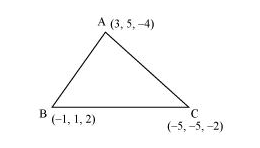
The direction ratios of side AB are (−1 − 3), (1 − 5), and (2 − (−4)) i.e., −4, −4, and 6.

Then, $\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}=\sqrt{16+16+36}$

$=\sqrt{68}$

$=2 \sqrt{17}$

Therefore, the direction cosines of AB are

$\frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}, \frac{6}{\sqrt{(-4)^{2}+(-4)^{2}+(6)^{2}}}$

$\frac{-4}{2 \sqrt{17}},-\frac{4}{2 \sqrt{17}}, \frac{6}{2 \sqrt{17}}$

$\frac{-2}{\sqrt{17}}, \frac{-2}{\sqrt{17}}, \frac{3}{\sqrt{17}}$

The direction ratios of BC are (−5 − (−1)), (−5 − 1), and (−2 − 2) i.e., −4, −6, and −4.

Therefore, the direction cosines of BC are

$\frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-6}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}, \frac{-4}{\sqrt{(-4)^{2}+(-6)^{2}+(-4)^{2}}}$

$\frac{-4}{2 \sqrt{17}}, \frac{-6}{2 \sqrt{17}}, \frac{-4}{2 \sqrt{17}}$

$\frac{-2}{\sqrt{17}}, \frac{-3}{\sqrt{17}}, \frac{-2}{\sqrt{17}}$

The direction ratios of CA are 3−(−5), 5−(−5) and −4−(−2) i.e. 8, 10 and -2.

Therefore the direction cosines of CA are

$\frac{8}{\sqrt{(8)^{2}+(10)^{2}+(-2)^{2}}}, \frac{10}{\sqrt{(8)^{2}+(10)^{2}+(-2)^{2}}}, \frac{-2}{\sqrt{(8)^{2}+(10)^{2}+(-2)^{2}}}$

$\frac{8}{2 \sqrt{42}}, \frac{10}{2 \sqrt{42}}, \frac{-2}{2 \sqrt{42}}$

$\frac{4}{\sqrt{42}}, \frac{5}{\sqrt{42}}, \frac{-1}{\sqrt{42}}$