Find the distance between the parallel lines

Given: parallel lines $4 x-3 y+5=0$ and $4 x-3 y+7=0$

To find : distance between the parallel lines

Formula used: The distance between the parallel lines $a x+b y+c=0$ and $a x+b y+d$ $=0$ is,

$D=\frac{|d-c|}{\sqrt{a^{2}+b^{2}}}$

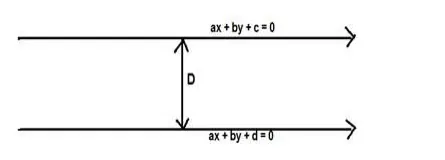
Here $a=4, b=-3, c=5, d=7$

$D=\frac{|7-5|}{\sqrt{4^{2}+(-3)^{2}}}=\frac{|2|}{\sqrt{16+9}}=\frac{2}{\sqrt{25}}=\frac{2}{5}$

The distance between the parallel lines $4 x-3 y+5=0$ and $4 x-3 y+7=0$ is $\frac{2}{5}$ units