Find the distance between the parallel lines p

Given: parallel lines $p(x+y)=q=0$ and $p(x+y)-r=0$

To find : distance between the parallel lines $p(x+y)-q=0$ and $p(x+y)-r=0$

Formula used: The distance between the parallel lines $a x+b y+c=0$ and $a x+b y+d$ $=0$ is,

$D=\frac{|d-c|}{\sqrt{a^{2}+b^{2}}}$

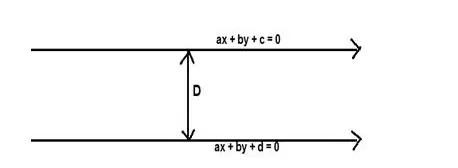
The parallel lines are $p(x+y)-q=0$ and $p(x+y)-r=0$

The parallel lines are $p x+p y-q=0$ and $p x+p y-r=0$

Here $a=p, b=p, c=-q, d=-r$

$D=\frac{|-r-(-q)|}{\sqrt{p^{2}+p^{2}}}=\frac{|-r+q|}{\sqrt{2 p^{2}}}=\frac{|q-r|}{p \sqrt{2}}$

The distance between the parallel lines $p(x+y)=q=0$ and $p(x+y)-r=0$ is $\frac{|q-1|}{p \sqrt{2}}$ units