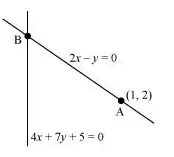
Find the distance of the line 4x + 7y + 5 = 0 from

The given lines are

2x – y = 0 … (1)

4x + 7y + 5 = 0 … (2)

A (1, 2) is a point on line (1).

Let B be the point of intersection of lines (1) and (2).

On solving equations (1) and (2), we obtain $x=\frac{-5}{18}$ and $y=\frac{-5}{9}$.

$\therefore$ Coordinates of point B are $\left(\frac{-5}{18}, \frac{-5}{9}\right)$.

By using distance formula, the distance between points A and B can be obtained as

$\mathrm{AB}=\sqrt{\left(1+\frac{5}{18}\right)^{2}+\left(2+\frac{5}{9}\right)^{2}}$ units

$=\sqrt{\left(\frac{23}{18}\right)^{2}+\left(\frac{23}{9}\right)^{2}}$ units

$=\sqrt{\left(\frac{23}{2 \times 9}\right)^{2}+\left(\frac{23}{9}\right)^{2}}$ units

$=\sqrt{\left(\frac{23}{9}\right)^{2}\left(\frac{1}{2}\right)^{2}+\left(\frac{23}{9}\right)^{2}}$ units

$=\sqrt{\left(\frac{23}{9}\right)^{2}\left(\frac{1}{4}+1\right) \text { units }}$

$=\sqrt{\left(\frac{23}{9}\right)^{2}\left(\frac{1}{4}+1\right)}$ units

$=\frac{23}{9} \sqrt{\frac{5}{4}}$ units

$=\frac{23}{9} \times \frac{\sqrt{5}}{2}$ units

$=\frac{23 \sqrt{5}}{18}$ units

Thus, the required distance is $\frac{23 \sqrt{5}}{18}$ units