Find the distance of the point

Given: Point $(-2,3)$ and line $12 x-5 y=13$

To find: The distance of the point $(-2,3)$ from the line $12 x-5 y=13$

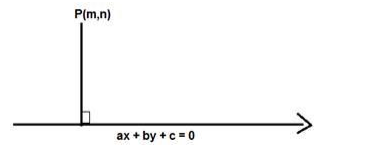
Formula used: We know that the distance between a point $P(m, n)$ and a line $a x+b y+$ $c=0$ is given by,

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

The given equation of the line is $12 x-5 y-13=0$

Here $m=-2$ and $n=3, a=12, b=-5, c=-13$

$D=\frac{|12(-2)-5(3)-13|}{\sqrt{12^{2}+5^{2}}}$

$D=\frac{|-24-15-13|}{\sqrt{144+25}}=\frac{|-52|}{\sqrt{169}}=\frac{|-52|}{13}=\frac{52}{13}=4$

D = 4

The distance of the point $(-2,3)$ from the line $12 x=5 y+13$ is 4 units