Find the domain and range of the real function, defined

For domain $\left(1+x^{2}\right) \neq 0$

$\Rightarrow x^{2} \neq-1$

$\Rightarrow \mathrm{dom}(\mathrm{f})=\mathrm{R}$

For the range of $x$ :

$\Rightarrow y=\frac{x^{2}+1-1}{x^{2}+1}=1-\frac{1}{x^{2}+1}$

$y_{\min }=0($ when $x=0)$

$y_{\max }=1(w h e n x=\infty)$

$\therefore$ range of $f(x)=[0,1)$

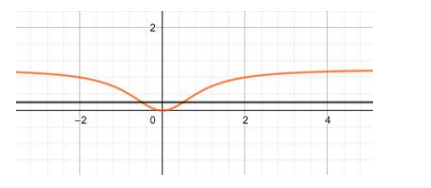
For many one the lines cut the curve in 2 equal valued points of y therefore the function f(x) $=\frac{x^{2}}{x^{2}+1}$ is many - one.

Ans:

$\operatorname{dom}(f)=R$

range $(f)=[0,1)$

function $f(x)=\frac{x^{2}}{x^{2}+1}$ is many - one.