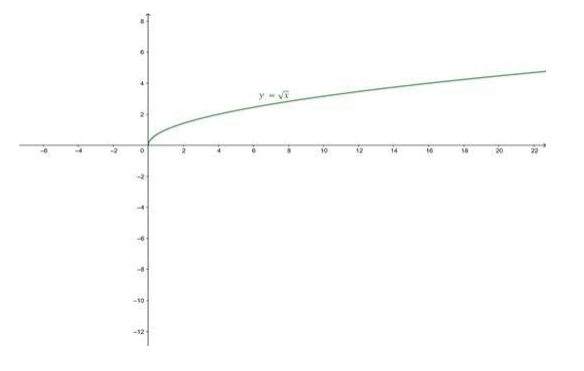
Find the domain and the range of the square root function,
f: $\mathbf{R}^{+} U\{0\} \rightarrow \mathbf{R} \mathbf{f}(\mathbf{x})=\sqrt{x}$ for all non-negative real numbers. Also, draw its graph.
Given
$f(x)=\sqrt{x}$
To Find: Domain and Range of $\mathrm{f}(\mathrm{x})$.
The domain of the given function is set of all positive real
Numbers including 0 . In this case, if the value of $x$ is a negative
The number then it makes the expression undefined.
Therefore,
Domain(f) $=[0, \infty) \forall x \in R^{+} \cup\{0\}$
As the value of $x$ varies from 0 to $\infty$, value of $\sqrt{x}$ varies from $\sqrt{0}$ to $\sqrt{\infty}$, Hence,
Range $(f)=[0, \infty) \forall x \in R^{+} \cup\{0\}$
Graph:
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
