Find the equation of the circle passing through the point

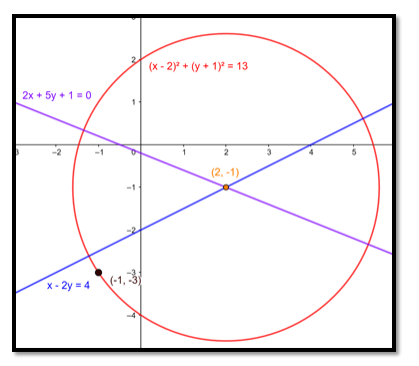
The intersection of the lines: $x-2 y=4$ and $2 x+5 y+1=0$.

is $(2,-1)$

$\therefore$ This problem is same as solving a circle equation with centre and point on the circle given.

The general form of the equation of a circle is:

$(x-h)^{2}+(y-k)^{2}=r^{2}$

Where, (h, k) is the centre of the circle.

r is the radius of the circle.

In this question we know that $(h, k)=(2,-1)$, so for determining the equation of the circle we need to determine the radius of the circle.

Since the circle passes through $(-1,-3)$, that pair of values for $x$ and $y$ must satisfy the equation and we have:

$\Rightarrow(-1-2)^{2}+(-3-(-1))^{2}=r^{2}$

$\Rightarrow(-3)^{2}+(-2)^{2}=r^{2}$

$\Rightarrow r^{2}=9+4=13$

$\therefore r^{2}=13$

⇒ Equation of circle is:

$(x-2)^{2}+(y-(-1))^{2}=13$

$\Rightarrow(x-2)^{2}+(y+1)^{2}=13$

Ans: $(x-2)^{2}+(y+1)^{2}=13$