Find the equation of the ellipse which passes through the point

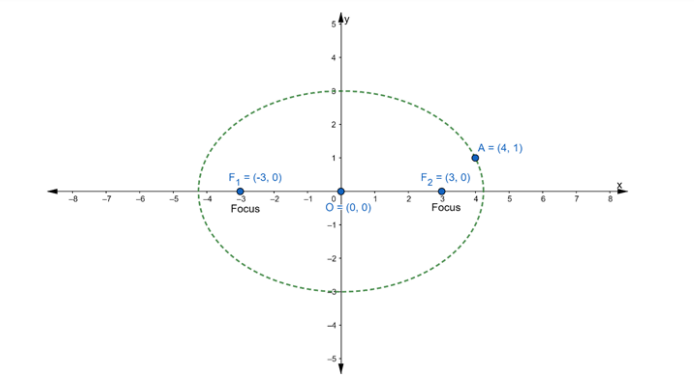
Let the equation of the required ellipse be

$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$  …(i)

Given:

Coordinates of foci $=(\pm 3,0)$...(ii)

We know that,

Coordinates of foci $=(\pm C, 0)$...(iii)

$\therefore$ From eq. (ii) and (iii), we get

c = 3

We know that,

$c^{2}=a^{2}-b^{2}$

$\Rightarrow(3)^{2}=a^{2}-b^{2}$

$\Rightarrow 9=a^{2}-b^{2}$

$\Rightarrow b^{2}=a^{2}-9 \ldots$ (iv)

Given that ellipse passing through the points $(4,1)$

So, point $(4,1)$ will satisfy the eq. (i)

Taking point $(4,1)$ where $x=4$ and $y=1$

Putting the values in eq. (i), we get

$\frac{(4)^{2}}{a^{2}}+\frac{(1)^{2}}{b^{2}}=1$

$\Rightarrow \frac{16}{a^{2}}+\frac{1}{b^{2}}=1$

$\Rightarrow \frac{16}{a^{2}}+\frac{1}{a^{2}-9}=1[$ from (iv) $]$

$\Rightarrow \frac{16\left(a^{2}-9\right)+a^{2}}{\left(a^{2}\right)\left(a^{2}-9\right)}=1$

$\Rightarrow 16 a^{2}-144+a^{2}=a^{2}\left(a^{2}-9\right)$

$\Rightarrow 17 a^{2}-144=a^{4}-9 a^{2}$

$\Rightarrow a^{4}-9 a^{2}-17 a^{2}+144=0$

$\Rightarrow a^{4}-26 a^{2}+144=0$

$\Rightarrow a^{4}-8 a^{2}-18 a^{2}+144=0$

$\Rightarrow a^{2}\left(a^{2}-8\right)-18\left(a^{2}-8\right)=0$

$\Rightarrow\left(a^{2}-8\right)\left(a^{2}-18\right)=0$

$\Rightarrow a^{2}-8=0$ or $a^{2}-18=0$

$\Rightarrow a^{2}=8$ or $a^{2}=18$

If $a^{2}=8$ then

$b^{2}=8-9$

$=-1$

Since the square of a real number cannot be negative. So, this is not possible

If $a^{2}=18$ then

$b^{2}=18-9$

= 9

So, equation of ellipse if $a^{2}=18$ and $b^{2}=9$

$\frac{x^{2}}{18}+\frac{y^{2}}{9}=1$