Find the equation of the ellipse whose foci are at (0, ±4) and

Given:

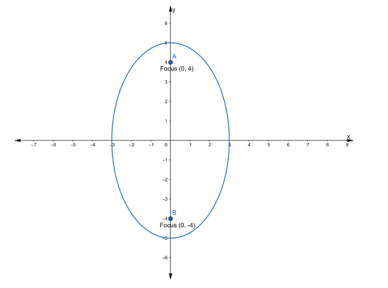
Coordinates of foci $=(0, \pm 4) \ldots$ (i)

We know that,

Coordinates of foci $=(0, \pm c) \ldots$ (ii)

The coordinates of the foci are $(0, \pm 4)$. This means that the major and minor axes are along $y$ and $x$ axes respectively.

$\therefore$ From eq. (i) and (ii), we get

c = 4

It is also given that

Eccentricity $=\frac{4}{5}$

we know that,

Eccentricity, $e=\frac{c}{a}$

$\Rightarrow \frac{4}{5}=\frac{4}{a}[\because c=4]$

$\Rightarrow a=5$

Now, we know that,

$c^{2}=a^{2}-b^{2}$

$\Rightarrow(4)^{2}=(5)^{2}-b^{2}$

$\Rightarrow 16=25-b^{2}$

$\Rightarrow b^{2}=25-16$

$\Rightarrow b^{2}=9$

Since, the foci of the ellipse are on $y$-axis. So, the Equation of Ellipse is

$\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1$

Substituting the value of $a^{2}$ and $b^{2}$, we get

$\Rightarrow \frac{x^{2}}{9}+\frac{y^{2}}{25}=1$