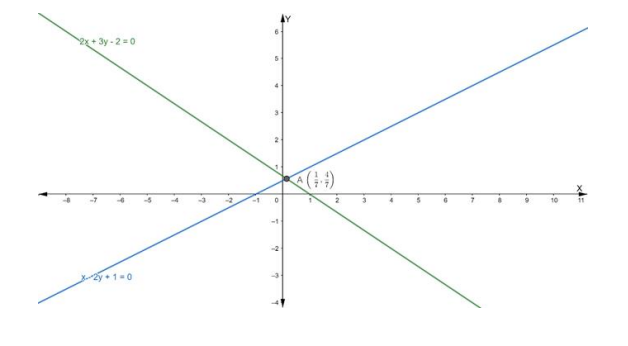
Find the equation of the line through the intersection of the lines

Suppose the given two lines intersect at a point $P\left(x_{1}, y_{1}\right) .$ Then, $\left(x_{1}, y_{1}\right)$ satisfies each of the given equations.

$2 x+3 y-2=0 \ldots$ (i)

$x-2 y+1=0 \ldots$ (ii)

Now, we find the point of intersection of eq. (i) and (ii)

Multiply the eq. (ii) by 2, we get

$2 x-4 y+2=0 \ldots$ (iii)

On subtracting eq. (iii) from (i), we get

$2 x+3 y-2-2 x+4 y-2=0$

$\Rightarrow 7 y-4=0$

$\Rightarrow 7 y=4$

$\Rightarrow \mathrm{y}=\frac{4}{7}$

Putting the value of y in eq. (ii), we get

$x-2\left(\frac{4}{7}\right)+1=0$

$\Rightarrow x-\frac{8}{7}+1=0$

$\Rightarrow x=\frac{8}{7}-1$

$\Rightarrow x=\frac{1}{7}$

Hence, the point of intersection $P\left(x_{1}, y_{1}\right)$ is

$\left(\frac{1}{7}, \frac{4}{7}\right)$

Now, the equation of a line in intercept form is:

$\frac{x}{a}+\frac{y}{b}=1$

where $a$ and $b$ are the intercepts on the axis.

Given that: $a=3$

$\Rightarrow \frac{x}{3}+\frac{y}{b}=1$

$\Rightarrow \frac{b x+3 y}{3 b}=1$

$\Rightarrow \mathrm{bx}+3 \mathrm{y}=3 \mathrm{~b} \ldots$ (i)

If eq. (i) passes through the point $\left(\frac{1}{7}, \frac{4}{7}\right)$, we get

$\mathrm{b}\left(\frac{1}{7}\right)+3\left(\frac{4}{7}\right)=3 \mathrm{~b}$

$\Rightarrow \frac{\mathrm{b}+12}{7}=3 \mathrm{~b}$

$\Rightarrow \mathrm{b}+12=21 \mathrm{~b}$

$\Rightarrow \mathrm{b}-21 \mathrm{~b}=-12$

$\Rightarrow 20 \mathrm{~b}=12$

$\Rightarrow \mathrm{b}=\frac{12}{20}=\frac{3}{5}$

Putting the value of ' $b$ ' in eq. (i), we get

$\frac{3}{5} \mathrm{x}+3 \mathrm{y}=3 \times \frac{3}{5}$

$\Rightarrow \frac{3}{5} \mathrm{x}+3 \mathrm{y}=\frac{9}{5}$

$\Rightarrow 3 x+15 y=9$

$\Rightarrow x+5 y=3$

Hence, the required equation of line is x + 5y = 3