`
Find the equation of the line which is at a distance of 3 units from the origin such that tan $\propto=\frac{5}{12}$
here ∝ is the acute angle which this perpendicular makes with the positive direction of the x-axis.
To Find:The equation of the line.
Given : $\propto=\frac{5}{12}$ and $p=3$ units.
Since $\tan \alpha=\frac{\text { opp }}{\text { adj }}=\frac{5}{12}$
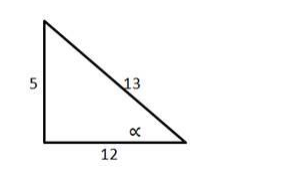
Using Pythagoras theorem :
hyp $=\sqrt{25+144}=\sqrt{169}=13$ units.
From the figure: $\cos \propto=\frac{\text { adj }}{\text { hyp }}=\frac{12}{13}$ and $\sin \propto=\frac{\text { opp }}{\text { hyp }}=\frac{5}{13}$
Formula used:
equation of the line: $x \cos \alpha+y \sin \propto=p$
$x \times\left(\frac{12}{13}\right)+y \times\left(\frac{5}{13}\right)=5$
Hence, $12 x+5 y=65$ is the required equation of the line.
.jpg)