Question:
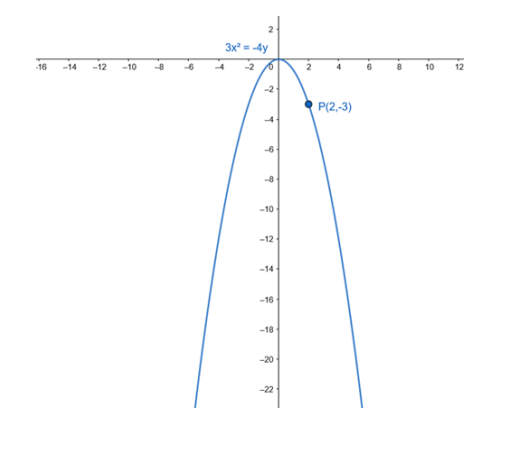
Find the equation of the parabola, which is symmetric about the y-axis and passes through the point P(2, -3).
Solution:
The equation of a parabola with vertex at the origin and symmetric about the y-axis is
$x^{2}=4 a y$
Since point $P(2,-3)$ passes through above parabola we can write,
$2^{2}=4 a(-3)$
$-4=-12 \mathrm{a}$
$\cdot a=-\frac{1}{3}$
Therefore, the equation of a parabola is
$x^{2}=4 \cdot\left(-\frac{1}{3}\right) y$
$x^{2}=-\frac{4}{3} y$
- $3 x^{2}=-4 y$
