Question:
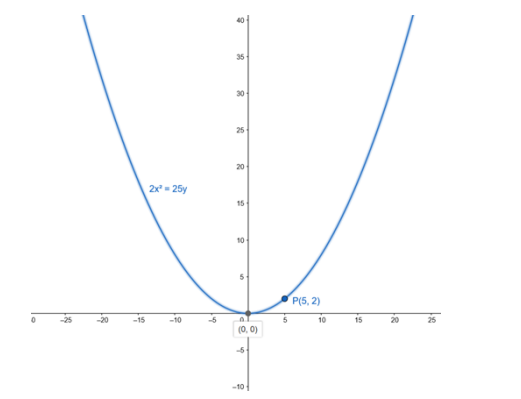
Find the equation of the parabola with vertex at the origin, passing through the point P(5, 2) and symmetric with respect to the y-axis.
Solution:
The equation of a parabola with vertex at the origin and symmetric about the y-axis is
$x^{2}=4 a y$
Since point P(5,2) passes through above parabola we can write,
$5^{2}=4 a(2)$
$\cdot 25=8 a$
$a=\frac{25}{8}$
Therefore, the equation of a parabola is
$x^{2}=4 \cdot \frac{25}{8} y$
$x^{2}=\frac{25}{2} y$
- $2 x^{2}=25 y$
