Find the image of the point

Let line AB be x – 3y + 4 = 0 and point P be (1, 2)

Let the image of the point P(1, 2) in the line mirror AB be Q(h, k)

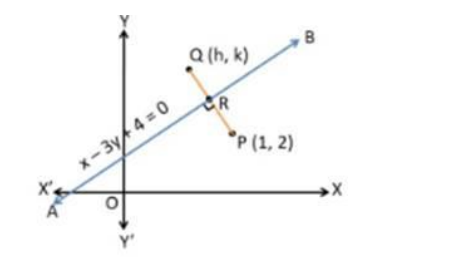
Since line $A B$ is a mirror. Then $P Q$ is perpendicularly bisected at $R$.

Since $R$ is the midpoint of $P Q$.

We know that,

Midpoint of a line joining $\left(x_{1}, y_{1}\right) \&\left(x_{2}, y_{2}\right)=\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}$

So, Midpoint of the line joining $(1,2) \&(h, k)=\frac{1+h}{2}, \frac{2+k}{2}$

Since point $R$ lies on the line $A B$. So, it will satisfy the equation of line $A B x-3 y+4=0$

Substituting the $\mathrm{x}=\frac{1+\mathrm{h}}{2} \& \mathrm{y}=\frac{2+\mathrm{k}}{2}$ in abthe ove equation, we get

$\frac{1+\mathrm{h}}{2}-3\left(\frac{2+\mathrm{k}}{2}\right)+4=0$

$\Rightarrow \frac{1+\mathrm{h}-6-3 \mathrm{k}+8}{2}=0$

$\Rightarrow 3+\mathrm{h}-3 \mathrm{k}=0$

$\Rightarrow \mathrm{h}-3 \mathrm{k}=-3 \ldots$ (i)

Also, $P Q$ is perpendicular to $A B$

We know that, if two lines are perpendicular then the product of their slope is equal to $-1$

$\therefore$ Slope of $A B \times$ Slope of $P Q=-1$

$\Rightarrow$ Slope of PQ $=\frac{-1}{\text { Slope of AB }}$

Now, we find the slope of line $A B$ i.e. $x-3 y+4=0$

We know that, the slope of an equation is

$\mathrm{m}=-\frac{\mathrm{a}}{\mathrm{b}}$

and here, $a=1 \& b=-3$

$\Rightarrow \mathrm{m}=-\frac{1}{(-3)}=\frac{1}{3}$

$=\frac{-1}{\frac{1}{3}}$

$=-3$

Now, Equation of line $P Q$ formed by joining the points $P(1,2)$ and $Q(h, k)$ and having the slope $-3$ is

$y_{2}-y_{1}=m\left(x_{2}-x_{1}\right)$

$\Rightarrow \mathrm{k}-2=(-3)(\mathrm{h}-1)$

$\Rightarrow \mathrm{k}-2=-3 \mathrm{~h}+3$

$\Rightarrow 3 \mathrm{~h}+\mathrm{k}=5 \ldots$ (ii)

Now, we will solve the eq. (i) and (ii) to find the value of h and k

$\mathrm{h}-3 \mathrm{k}=-3 \ldots(\mathrm{i})$

and $3 h+k=5 \ldots$ (ii)

From eq. (i), we get

$h=-3+3 k$

Putting the value of h in eq. (ii), we get

$3(-3+3 k)+k=5$

$\Rightarrow-9+9 k+k=5$

$\Rightarrow-9+10 k=5$

$\Rightarrow 10 k=5+9$

$\Rightarrow 10 k=14$

$\Rightarrow \mathrm{k}=\frac{14}{10}=\frac{7}{5}$

Putting the value of k in eq. (i), we get

$h-3\left(\frac{7}{5}\right)=-3$

$\Rightarrow 5 \mathrm{~h}-21=-3 \times 5$

$\Rightarrow 5 \mathrm{~h}-21=-15$

$\Rightarrow 5 \mathrm{~h}=-15+21$

$\Rightarrow 5 \mathrm{~h}=6$

$\Rightarrow \mathrm{h}=\frac{6}{5}$