Find the length of a chord which is at a distance of 3 cm from the centre of a circle of radius 5 cm.

Let AB be the chord of the given circle with centre O and a radius of 5 cm.
From O, draw OM perpendicular to AB.
Then OM = 3 cm and OB = 5 cm

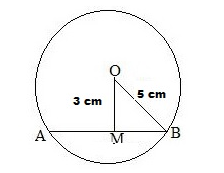
From the right ΔOMB, we have:
OB2 = OM2 + MB2        (Pythagoras theorem)
⇒ 52 = 32 + MB2
⇒ 25 = 9 + MB2
⇒ MB2 = (25 − 9) = 16

$\Rightarrow M B=\sqrt{16} \mathrm{~cm}=4 \mathrm{~cm}$

Since the perpendicular from the centre of a circle to a chord bisects the chord, we have:
AB = 2 × MB = (2 × 4) cm = 8 cm
Hence, the required length of the chord is 8 cm.