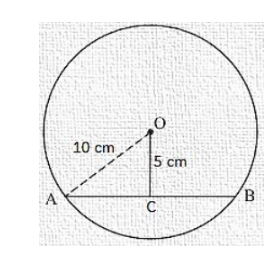
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.

Solution:

Given that,

Distance (OC) = 5 cm

Radius of the circle (OA) = 10 cm

In ΔOCA, by Pythagoras theorem

$O C^{2}+A C^{2}=O A^{2}$

$\Rightarrow 5^{2}+A C^{2}=10^{2}$

$\Rightarrow 25+A C^{2}=100$

$\Rightarrow A C^{2}=100-25$

$\Rightarrow A C^{2}=75$

$\Rightarrow \mathrm{AC}=\sqrt{75}$

We know that, the perpendicular from the centre to chord bisects the chord

Therefore, AC = BC = 8.66cm

Then the chord AB = 8.66 + 8.66

= 17.32 cm