Find the length of a tangent drawn to a circle with radius 5 cm,

Let us first put the given data in the form of a diagram.

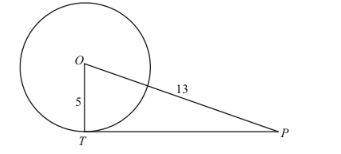
We have to find TP. From the properties of tangents we know that a tangent will always be at right angles to the radius of the circle at the point of contact. Therefore is a right angle and triangle OTP is a right triangle.

We can find the length of TP using Pythagoras theorem. We have,

$T P^{2}=O P^{2}-O T^{2}$

$T P^{2}=13^{2}-5^{2}$

$T P^{2}=(13-5)(13+5)$

$T P^{2}=8 \times 18$

$T P^{2}=144$

$T P=\sqrt{144}$

$T P=12$

Therefore, the length of $T P$ is $12 \mathrm{~cm}$.