Find the length of the altitude of an equilateral triangle of side 2a cm.

Let the triangle be ABC with AD as its altitude. Then, D is the midpoint of BC.
In right-angled triangle ABD, we have:

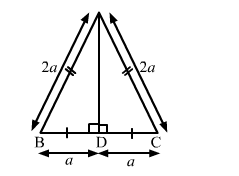
$A B^{2}=A D^{2}+D B^{2}$

$\Rightarrow A D^{2}=A B^{2}-D B^{2}=4 a^{2}-a^{2} \quad\left(\because B D=\frac{1}{2} B C\right)$

$=3 a^{2}$

$A D=\sqrt{3} a$

Hence, the length of the altitude of an equilateral triangle of side $2 a \mathrm{~cm}$ is $\sqrt{3} a \mathrm{~cm}$.