Find the lengths of the medians of the triangle with vertices A (0, 0, 6), B (0, 4, 0) and (6, 0, 0).

Let AD, BE, and CF be the medians of the given triangle ABC.

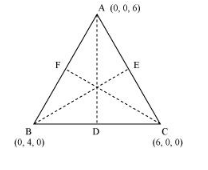
Since AD is the median, D is the mid-point of BC.

$\therefore$ Coordinates of point $D=\left(\frac{0+6}{2}, \frac{4+0}{2}, \frac{0+0}{2}\right)=(3,2,0)$

$\mathrm{AD}=\sqrt{(0-3)^{2}+(0-2)^{2}+(6-0)^{2}}=\sqrt{9+4+36}=\sqrt{49}=7$

Since $B E$ is the median, $E$ is the mid-point of $A C$.

$\therefore$ Coordinates of point $\mathrm{E}=\left(\frac{0+6}{2}, \frac{0+0}{2}, \frac{6+0}{2}\right)=(3,0,3)$

$B E=\sqrt{(3-0)^{2}+(0-4)^{2}+(3-0)^{2}}=\sqrt{9+16+9}=\sqrt{34}$

Since $\mathrm{CF}$ is the median, $\mathrm{F}$ is the mid-point of $\mathrm{AB}$.

$\therefore$ Coordinates of point $\mathrm{F}=\left(\frac{0+0}{2}, \frac{0+4}{2}, \frac{6+0}{2}\right)=(0,2,3)$

Length of $\mathrm{CF}=\sqrt{(6-0)^{2}+(0-2)^{2}+(0-3)^{2}}=\sqrt{36+4+9}=\sqrt{49}=7$

Thus, the lengths of the medians of $\triangle \mathrm{ABC}$ are $7, \sqrt{34}$, and 7 .