Find the linear inequalities for which the shaded area is the solution set in the figure given below.

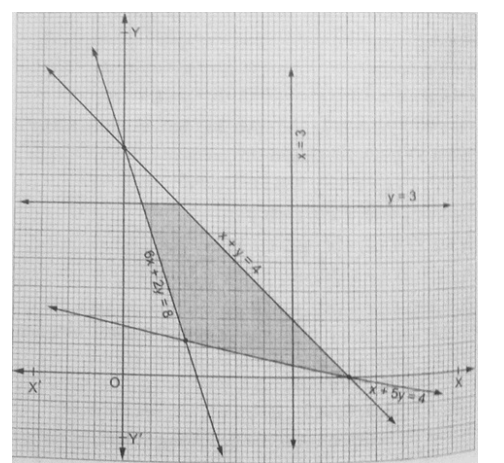
We have seen that the shaded region and origin are on the opposite side of the line $6 x+2 y=8$

For $(0,0)$ we have $0+0-8<0$. So the shaded region satisfies the inequality $6 x+2 y \geq 8$.

We have seen that the shaded region and origin are on the opposite side of the line $x+5 y=4$

For $(0,0)$ we have $0+0-4<0$. So the shaded region satisfies the inequality $x+5 y \geq 4$.

We have seen that the shaded region and origin are on the same side of the line $x+y=4$

For $(0,0)$ we have $0+0-4<0$. So the shaded region satisfies the inequality $\boldsymbol{x}+\boldsymbol{y} \leq \mathbf{4}$.

We have seen that the shaded region and origin are on the same side of the line $y=3$

For $(0,0)$ we have $0-3<0$. So the shaded region satisfies the inequality $y \leq 3$.

Thus the linear inequation comprising the given solution set are $+2 y \geq 8, x+5 y \geq 4, x+y \leq 4, y \leq 3$