Find the mean deviation about the median for the data

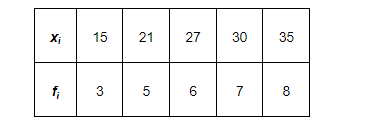
The given observations are already in ascending order.

Adding a column corresponding to cumulative frequencies of the given data, we obtain the following table.

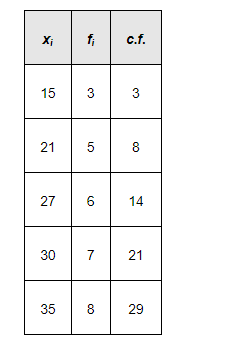
Here, $N=29$, which is odd.

$\therefore$ Median $=\left(\frac{29+1}{2}\right)^{\text {th }}$ observation $=15^{\text {th }}$ observation

This observation lies in the cumulative frequency 21, for which the corresponding observation is 30.

$\therefore$ Median $=30$

The absolute values of the deviations from median, i.e. $\left|x_{i}-\mathrm{M}\right|$, are

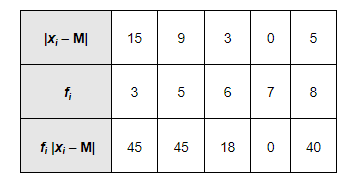
$\sum_{i=1}^{5} f_{i}=29, \sum_{i=1}^{5} f_{i}\left|x_{i}-\mathrm{M}\right|=148$

$\therefore$ M.D. $(\mathrm{M})=\frac{1}{\mathrm{~N}} \sum_{i=1}^{5} f_{i}\left|x_{i}-\mathrm{M}\right|=\frac{1}{29} \times 148=5.1$