Question:
Find the mean, variance and standard deviation using short-cut method
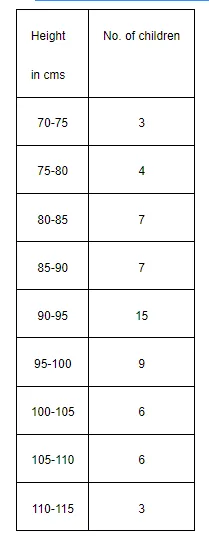
Solution:
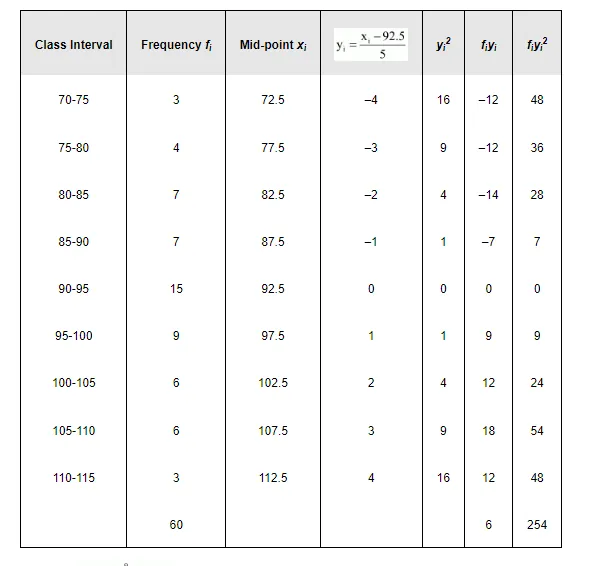
Mean, $\bar{x}=\mathrm{A}+\frac{\sum_{i=1}^{9} \mathrm{f}_{i} \mathrm{y}_{i}}{\mathrm{~N}} \times \mathrm{h}=92.5+\frac{6}{60} \times 5=92.5+0.5=93$
Variance $\left(\sigma^{2}\right)=\frac{h^{2}}{N^{2}}\left[N \sum_{i=1}^{g} f_{i} y_{i}{ }^{2}-\left(\sum_{i=1}^{g} f_{i} y_{i}\right)^{2}\right]$
$=\frac{(5)^{2}}{(60)^{2}}\left[60 \times 254-(6)^{2}\right]$
$=\frac{25}{3600}(15204)=105.58$
$\therefore$ Stan dard deviation $(\sigma)=\sqrt{105.58}=10.27$
