Find the missing value of p for the following distribution whose mean is 12.58

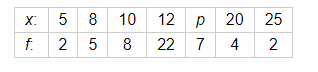
Given:

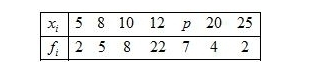
Mean $=12.58$

First of all prepare the frequency table in such a way that its first column consist of the values of the variate $\left(x_{i}\right)$ and the second column the corresponding frequencies $\left(f_{i}\right)$.

Thereafter multiply the frequency of each row with corresponding values of variable to obtain third column containing $\left(f_{i} x_{i}\right)$.

Then, sum of all entries in the column second and denoted by $\sum f_{i}$ and in the third column to obtain $\sum f_{i} x_{i}$.

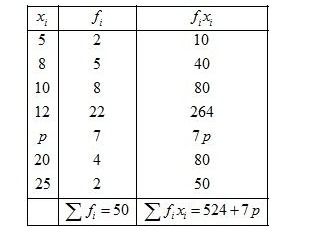
We know that mean, $\bar{X}=\frac{\sum f_{i} x_{i}}{\sum f_{i}}$

$12.58=\frac{524+7 p}{50}$

By using cross multiplication method

$524+7 p=12.58 \times 50$

$7 p=629-524$

$=\frac{105}{7}$

$=15$

Hence, $p=15$