Find the number of permutations of the letters of the word ‘ENGLISH’.

There are 7 letters in the word ENGLISH.

Permutation of 7 letters in 7 places can be done in $\mathrm{P}(7,7)$ ways.

Formula:

Number of permutations of n distinct objects among r different places, where repetition is not allowed, is

$P(n, r)=n ! /(n-r) !$

Therefore, a permutation of 7 different objects in 7 places is

$P(7,7)=\frac{7 !}{(7-7) !}=\frac{7 !}{0 !}=\frac{5040}{1}=5040$

Hence, the total number of permutations is P 5040.

To find a number of words starting with $E$ and ending with $I$, let us consider their position which is $1^{\text {st }}$ and $7^{\text {th }}$.

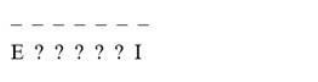
The rest 5 letters are to be arranged in 5 places which can be done in P (5,5)

Formula:

Number of permutations of $n$ distinct objects among $r$ different places, where repetition is not allowed, is

$P(n, r)=n ! /(n-r) !$

Therefore, a permutation of 5 different objects in 5 places is

$P(5,5)=\frac{5 !}{(5-5) !}=\frac{5 !}{0 !}=\frac{120}{1}=120$

Therefore, there are 120 words starting with E and ending with I