Find the pair of similar triangles among the given pairs.

Solution:

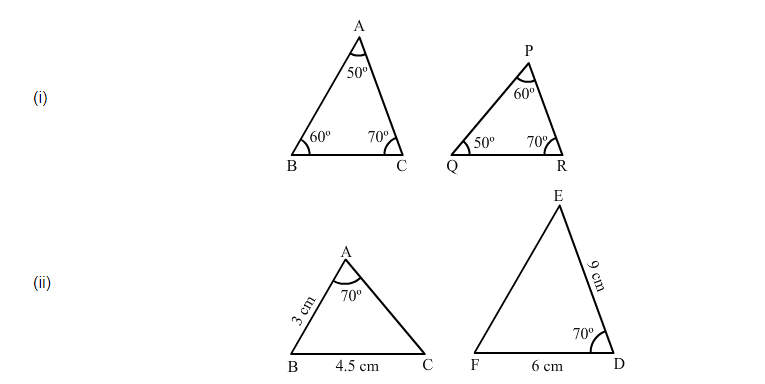
(i)
We have:

$\angle B A C=\angle P Q R=50^{\circ}$

$\angle A B C=\angle Q P R=60^{\circ}$

 

$\angle A C B=\angle P R Q=70^{\circ}$

Therefore, by AAA similarity theorem, $\triangle A B C \sim Q P R$

(ii)
We have:

$\frac{A B}{D F}=\frac{3}{6}=\frac{1}{2}$ and $\frac{B C}{D E}=\frac{4.5}{9}=\frac{1}{2}$

But, $\angle A B C \neq \angle E D F$ (Included angles are not equal)

Thus, this does not satisfy SAS similarity theorem.
Hence, the triangles are not similar.

(iii)
We have:

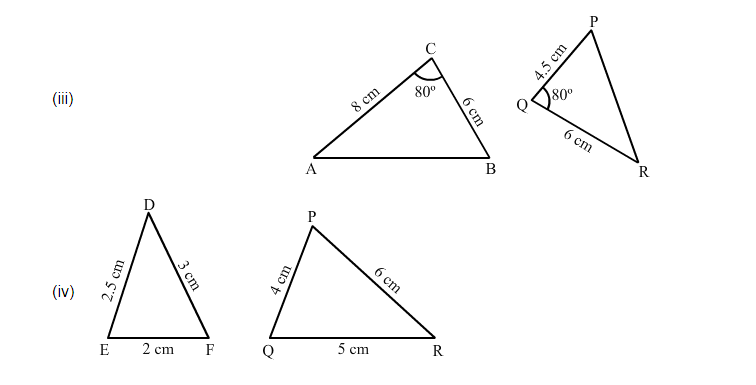
$\frac{C A}{Q R}=\frac{8}{6}=\frac{4}{3}$ and $\frac{C B}{P Q}=\frac{6}{4.5}=\frac{4}{3}$

$\Rightarrow \frac{C A}{Q R}=\frac{C B}{P Q}$

Also, $\angle A C B=\angle P Q R=80^{\circ}$

Therefore, by SAS similarity theorem, $\triangle A C B \sim \triangle R Q P$.

(iv)
 We have

$\frac{D E}{Q R}=\frac{2.5}{5}=\frac{1}{2}$

$\frac{E F}{P Q}=\frac{2}{4}=\frac{1}{2}$

$\frac{D F}{P R}=\frac{3}{6}=\frac{1}{2}$

$\Rightarrow \frac{D E}{Q R}=\frac{E F}{P Q}=\frac{D F}{P R}$

Therefore, by SSS similarity theorem, $\triangle F E D \sim \triangle P Q R$

(v)

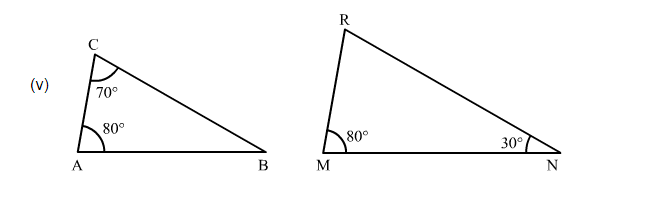
In $\triangle \mathrm{ABC}$

$\angle \mathrm{A}+\angle \mathrm{B}+\angle \mathrm{C}=180^{\circ} \quad$ (Angle Sum Property)

$\Rightarrow 80^{\circ}+\angle B+70^{\circ}=180^{\circ}$

$\Rightarrow \angle \mathrm{B}=30^{\circ}$

$\angle \mathrm{A}=\angle \mathrm{M}$ and $\angle \mathrm{B}=\angle \mathrm{N}$

Therefore, by AA similarity theorem, $\triangle \mathrm{ABC} \sim \triangle \mathrm{MNR}$