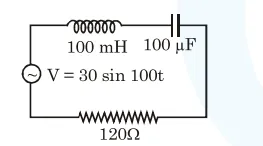
Find the peak current and resonant frequency of the following circuit (as shown in figure).

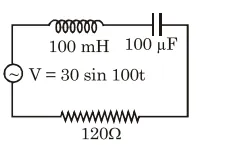
as given $\mathrm{z}=\sqrt{\left(\mathrm{x}_{\mathrm{L}}-\mathrm{x}_{\mathrm{C}}\right)^{2}+\mathrm{R}^{2}}$

$\mathrm{x}_{\mathrm{L}}=\omega_{\mathrm{L}}=100 \times 100 \times 10^{-3}=10 \Omega$

$\mathrm{x}_{\mathrm{C}}=\frac{1}{\omega_{\mathrm{C}}}=\frac{1}{100 \times 100 \times 10^{-6}}=10 \Omega$

$\mathrm{z}=\sqrt{(10-100)^{2}+\mathrm{R}^{2}}=\sqrt{90^{2}+120^{2}}$

$=30 \times 5=150 \Omega$

$\mathrm{i}_{\text {peak }}=\frac{\Delta \mathrm{v}}{\mathrm{z}}=\frac{30}{150}=\frac{1}{5} \mathrm{amp}=0.2 \mathrm{amp}$

\& For resonant frequency

$\Rightarrow \omega \mathrm{L}=\frac{1}{\omega \mathrm{C}} \Rightarrow \omega^{2}=\frac{1}{\mathrm{LC}} \Rightarrow \omega=\frac{1}{\sqrt{\mathrm{LC}}}$

$\& \mathrm{f}=\frac{1}{2 \pi \sqrt{\mathrm{LC}}} \Rightarrow \frac{1}{2 \pi \sqrt{100 \times 10^{-3} \times 100 \times 10^{-6}}}$

$=\frac{100 \sqrt{10}}{2 \pi}=\frac{100 \pi}{2 \pi}=50 \mathrm{~Hz}$

as $\sqrt{10} \approx \pi$

Answer (1)