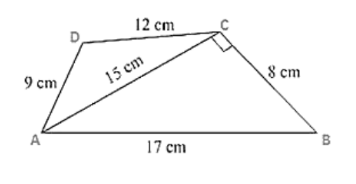
Find the perimeter and the area of the quadrilateral

Given are the sides of the quadrilateral ABCD in which

AB = 17 cm, AD = 9 cm, CD = 12 cm, AC = 15 cm and an angle ACB = 90°

By using Pythagoras theorem

$B C^{2}=A B^{2}-A C^{2}$

$B C^{2}=17^{2}-15^{2}$

BC = 8 cm

Now, area of triangle $A B C=1 / 2 \times A C \times B C$

Area of triangle $\mathrm{ABC}=1 / 2 \times 8 \times 15$

Area of triangle $A B C=60 \mathrm{~cm}^{2}$

Now, for the area of triangle ACD

Perimeter of triangle ACD 2s = AC + CD + AD

2s = 15 + 12 + 9

s = 18 cm

By using Heron's Formula,

Area of the triangle $\mathrm{ACD}=\sqrt{s \times(s-a) \times(s-b) \times(s-c)}$

$=\sqrt{18 \times(3) \times(6) \times(9)}$

$=54 \mathrm{~cm}^{2}$

Area of quadrilateral ABCD = Area of triangle ABC + Area of triangle ACD

Area of quadrilateral $A B C D=60 \mathrm{~cm}^{2}+54 \mathrm{~cm}^{2}$

Area of quadrilateral $\mathrm{ABCD}=114 \mathrm{~cm}^{2}$