Find the point on the curve

Since, the tangent is parallel to $y$-axis, its slope is not defined, then the normal is parallel to $x$ - axis whose slope is zero.

$\mathrm{i} . e, \frac{-1}{\frac{\mathrm{d} y}{\mathrm{dx}}}=0$

$\Rightarrow \frac{-1}{\frac{1-x}{y}}=0$

$\Rightarrow \frac{-y}{1-x}=0$

$\Rightarrow y=0$

Substituting $y=0$ in $x^{2}+y^{2}-2 x-3=0$

$\Rightarrow x^{2}+0^{2}-2 x x-3=0$

$\Rightarrow x^{2}-2 x-3=0$'

Using factorization method, we can solve above quadratic equation

$\Rightarrow x^{2}-3 x+x-3=0$

$\Rightarrow x(x-3)+1(x-3)=0$

$\Rightarrow(x-3)(x+1)=0$

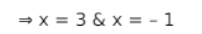
Thus, the required point is $(3,0) \&(-1,0)$