Find the range of each of the following functions.

(i) $f(x)=2-3 x, x \in \mathbf{R}, x>0$

The values of $f(x)$ for various values of real numbers $x>0$ can be written in the tabular form as

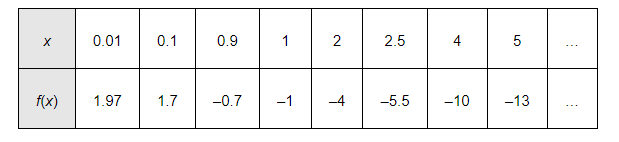
Thus, it can be clearly observed that the range of f is the set of all real numbers less than 2.

i.e., range of $f=(-\infty, 2)$

Alter:

Let $x>0$

$\Rightarrow 3 x>0$

$\Rightarrow 2-3 x<2$

$\Rightarrow f(x)<2$

$\therefore$ Range of $f=(-\infty, 2)$

(ii) $f(x)=x^{2}+2, x$, is a real number

The values of f(x) for various values of real numbers x can be written in the tabular form as

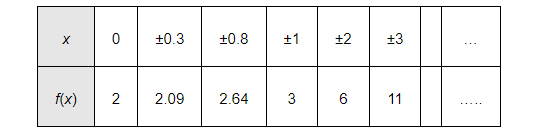
Thus, it can be clearly observed that the range of f is the set of all real numbers greater than 2.

i.e., range of $f=[2, \infty)$

Alter:

Let x be any real number.

      Accordingly,

$x^{2} \geq 0$

$\Rightarrow x^{2}+2 \geq 0+2$

$\Rightarrow x^{2}+2 \geq 2$

$\Rightarrow f(x) \geq 2$

$\therefore$ Range of $f=[2, \infty)$

(iii) $f(x)=x, x$ is a real number

It is clear that the range of $f$ is the set of all real numbers.

$\therefore$ Range of $f=\mathbf{R}$