Find the remainder when $x^{3}+3 x^{2}+3 x+1$ is divided by <br/> <br/>(i) $x+1$ <br/> <br/>(ii) $x-\frac{1}{2}$ <br/> <br/>(iii) $x$(iv) $x+\pi$ <br/> <br/>(v) $5+2 x$
Solution:
(i) $x+1$
By long division,
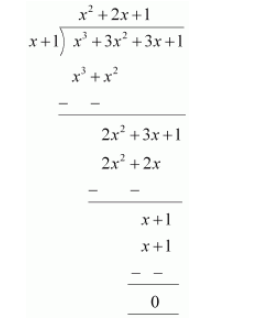
Therefore, the remainder is 0 .
(ii) $x-\frac{1}{2}$
By long division,

Therefore, the remainder is $\frac{27}{8}$.
(iii) $X$
By long division,

Therefore, the remainder is 1 .
(iv) $x+\pi$
By long division,

Therefore, the remainder is $-\pi^{3}+3 \pi^{2}-3 \pi+1$.
(v) $5+2 x$
By long division,

Therefore, the remainder is $-\frac{27}{8}$
(i) $x+1$
By long division,
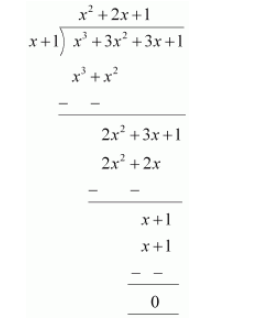
Therefore, the remainder is 0 .
(ii) $x-\frac{1}{2}$
By long division,

Therefore, the remainder is $\frac{27}{8}$.
(iii) $X$
By long division,

Therefore, the remainder is 1 .
(iv) $x+\pi$
By long division,

Therefore, the remainder is $-\pi^{3}+3 \pi^{2}-3 \pi+1$.
(v) $5+2 x$
By long division,

Therefore, the remainder is $-\frac{27}{8}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
