Find the solution of the pair of equations

Given pair of equations is

$\frac{x}{10}+\frac{y}{5}-1=0$ $\ldots($ i)

and $\frac{x}{8}+\frac{y}{6}=15$ .....(ii)

Now, multiplying both sides of Eq. (i) by LCM $(10,5)=10$, we get

$x+2 y-10=0$

$\Rightarrow$    $x+2 y=10$ ....(iii)

Again, multiplying both sides of Eq. (iv) by LCM $(8,6)=24$, we get

$3 x+4 y=360$   ...(iv)

On, multiplying Eq. (iii) by 2 and then subtracting from Eq. (iv), we get

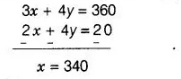
Put the value of $x$ in Eq. (iii), we get

$340+2 y=10$

$\Rightarrow \quad 2 y=10-340=-330$

$\Rightarrow \quad y=-165$

Given that, the linear relation between $x, y$ and $\lambda$ is

$y=\lambda x+5$

Now, put the values of $x$ and $y$ in above relation, we get

$-165=\lambda(340)+5$

$\Rightarrow \quad 340 \lambda=-170$

$\Rightarrow \quad \lambda=-\frac{1}{2}$

Hence, the solution of the pair of equations is $x=340, y=-165$ and the required value of $\lambda$ is $-\frac{1}{2}$