Find the sum of first 17 terms

Let the first term, common difference and the number of terms in an AP are a, d and n,respectively

We know that, the $n$th term of an AP, $T_{n}=a+(n-1) d$   $\ldots$ (i)

$\therefore \quad$ 4th term of an AP, $T_{4}=a+(4-1) d=-15$ [given]

$\Rightarrow \quad a+3 d=-15 \quad \ldots$ (ii)

and 9th term of an AP, $T_{a}=a+(9-1) d=-30$ [given]

$\Rightarrow \quad a+8 d=-30$ .....(iii)

Now, subtract Eq. (ii) from Eq. (iii), we get

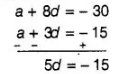
$\Rightarrow \quad d=-3$

Put the value of $d$ in Eq. (ii), we get 

$a+3(-3)=-15 \Rightarrow a-9=-15$

$\Rightarrow \quad a=-15+9 \Rightarrow a=-6$

$\because$ Sum of first $n$ terms of an AP, $S_{n}=\frac{n}{2}[2 a+(n-1) d]$

$\therefore$ Sum of first 17 terms of an AP, $S_{17}=\frac{17}{2}[2 \times(-6)+(17-1)(-3)]$

$=\frac{17}{2}[-12+(16)(-3)]$

$=\frac{17}{2}(-12-48)=\frac{17}{2} \times(-60)$

$=17 \times(-30)=-510$

Hence,the required sum of first 17 terms  of an AP is -510